Oscilloscope PCE-DSO 8060
oscilloscope avec un multimètre et un générateur de fonctions / écran TFT couleurs de 5,7" /
analyse FFT / haut part de mesure / port USB / accumulateur ion-lithium

L'oscilloscope PCE-DSO 8060 intègre 3 mesureurs en 1. En plus d'être un oscilloscope, il intègre un multimètre et un générateur de fonctions. L'oscilloscope PCE-DSO 8060 a été particulièrement conçu pour un usage mobile. Le grand écran LCD, qui intègre une illumination LED, est à lecture facile, même quand les rayons de soleil illuminent l'écran. Une anse située sur le côté de l'oscilloscope permet de porter cet instrument n'importe où. La protection en caoutchouc évite que pendant le transport ou la manipulation de l'oscilloscope, la carcasse soit endommagée. Cet oscilloscope à usage facile a des prestations semblables aux dispositifs de table. Il possède une largeur de bande de jusqu'à 60 MHz et une vitesse d'échantillonnage de jusqu'à 150 MS/s. En plus de la mesure simple de tous les paramètres des signaux d'entrée, l'oscilloscope effectue une analyse FFT. Tous les réglages de V / div, s / div ou de déclenchement du signal s'effectuent à travers des puiseurs en caoutchouc de l'oscilloscope. Les deux canaux d'entrée de l'oscilloscope PCE-DSO 8060 se connectent aux sondes à travers de connecteurs BNC. Les sondes inclues dans la livraison peuvent passe à un facteur de régulation de 1:1 ou de 10:1. L'oscilloscope permet aussi de sélectionner les différents modes d'opération. Une simple pulsation des touches suffit pour que l'oscilloscope se convertisse en un multimètre digital à différentes fonctions telles que la mesure de la tension ou de la capacité. La connexion des câbles d'essai pour le multimètre s'effectue à travers de connecteurs banane de 4 mm situés sur la face de l'oscilloscope. Le générateur de fonctions incorporé de l'oscilloscope PCE-DSO 8060 simule les formes d'onde que l'usager peut régler librement. En fait il crée des formes d'onde spiroïdales, des ondes triangulaires ou des ondes rectangulaires. Vous pouvez alimenter l'oscilloscope au secteur avec un composant inclus dans la livraison ou avec un accumulateur ion-lithium incorporé. La durée de l'accumulateur est d'environ 6 h en fonctionnement continu. Lors d'une utilisation de l'oscilloscope avec l'accumulateur veuillez tenir compte que l'écran se déconnecte après un certain temps d'inactivité pour prolonger la durée de vie de l'accumulateur. A travers l'un des deux ports USB vous pouvez connecter l'oscilloscope à l'ordinateur. Le second port permet à l'usager de garder directement les images qui apparaissent sur un crayon USB. Pour de plus amples informations en ce qui concerne l'oscilloscope, veuillez consulter la fiche technique ci-dessous ou nous contacter au +33 (0) 972 3537 17. Nos techniciens et ingénieurs seront heureux de vous conseiller sur cet oscilloscope ou sur tous les autres produits du domaine de la technologie de laboratoires, des systèmes de régulation et contrôle, des mesureurs ou des balances de PCE Instruments.

- Largeur de bande 60 MHz

- 150 MSamples

- Maximum de 300 V en mode oscilloscope

- Haute sensibilité

- De nombreuses fonctions mathématiques

- Grand écran LCD dans l'oscilloscope

- Multimètre intégré

- Générateur de fonctions

Caractéristiques techniques de l'oscilloscope PCE-DSO 8060

Composant vertical

Canaux

Deux

Largeur de bande

60 MHz

Flanc de remontée

5,8 nS

Impédance d'entrée

Résistance: 1 MΩ
Capacitif: 15 pF

Sensibilité d'entrée

10 mV/div ... 5 V/div

Accouplement d'entrée

AC, DC, GND

Résolution verticale de l'oscilloscope

8 bit

Mémoire

En mode 1 canal: 32 k
En mode 2 canaux: 16 k

Tension d'entrée max.

300 V (DC et pointe AC)

Composant horizontal

Vitesse d'échantillonnage

150 MSamples/s

Echantillonnage en temps équivalent

50 GSamples/s

Balayage

5 ns / div ... 1000 ns / div

Précision du balayage

± 50 ppm

Déclencheur (trigger)

Source

Canal 1
Canal 2
Externe

Mode

Rectangulaire
Impulsions en largeur
Alternatif

Mode X-Y

Axe X

Canal 1

Axe Y

Canal 2

Déplacement

Max. 3 º

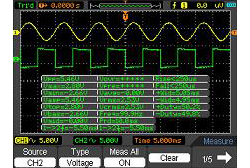
Fonction de mesure

Tension

V_pp, V_amp, V_máx., V_mín., V_top, V_mid, V_base, V_avg,
V_rms, V_crms, Preshoot, Overshoot

Temps

Fréquence, période, flanc de remontée, flanc de
téléchargement, cycle de travail (Duty Cycle)

Curseur

Manuel, exploration, automatique

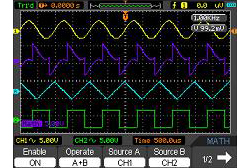
Fonction mathématique de l'oscilloscope

Addition, soustraction, multiplication, division, FFT

Mémoire

15 formes d'onde et configurations

Sondes d'essai

Facteur de régulation

1:1, 10:1 (pouvant se sélectionner)

Longueur du câble

Environ 1,2 m

Vous pouvez observer ici les fonctions
mathématiques de l'oscilloscope PCE-DSO 8060

En plus des courbes de mesure, l'oscilloscope
est capable de représenter tous les
paramètres sous forme numérique

Caractéristiques générales de la fonction multimètre de l'oscilloscope

Résolution maximum

6000 positions

Fonctions de mesure

Tension, courant, résistance, capacité,
test de diodes, test de continuité

Tension maximum d'entrée

600 V AC / 800 V DC

Courant maximum d'entrée

10 A AC / 10 A DC

Impédance d'entrée

10 MΩ

Caractéristiques techniques de la fonction multimètre de l'oscilloscope PCE-DSO 8060

Plage de mesure

Résolution

Précision

Tension continue

60 mV

10 µV

±1 % ±1 digit

600 mV

100 µV

±1 % ±1 digit

6 V

1 mV

±1 % ±1 digit

60 V

10 mV

±1 % ±1 digit

600 V

100 mV

±1 % ±1 digit

800 V

1 V

±1 % ±1 digit

Tension alternative

60 mV

10 µV

±1 % ±3 digits

600 mV

100 µV

±1 % ±3 digits

6 V

1 mV

±1 % ±3 digits

60 V

10 mV

±1 % ±3 digits

600 V

100 mV

±1 % ±3 digits

Courant continu

60 mA

10 µA

±1,5 % ±1 digit

600 mA

100 µA

±1 % ±1 digit

6 A

1 mA

±1,5 % ±3 digits

10 A

10 mA

±1,5 % ±3 digits

Courant alternatif

60 mA

10 µA

±1,5 % ±3 digits

600 mA

100 µA

±1 % ±1 digit

6 A

1 mA

±1,5 % ±3 digits

10 A

10 mA

±1,5 % ±3 digits

Résistance

600 Ω

0,1 Ω

±1 % ±3 digits

6 kΩ

1 Ω

±1 % ±1 digit

60 kΩ

10 Ω

±1 % ±1 digit

6 MΩ

100 Ω

±1 % ±1 digit

60 MΩ

1 kΩ

±1,5 % ±3 digits

Capacité

40 nF

10 pF

±1 % ±1 digit

400 nF

100 pF

±1 % ±1 digit

4 µF

1 nF

±1 % ±1 digit

40 µF

10 nF

±1 % ±1 digit

400 µF

100 nF

±1 % ±1 digit

Avertissement:
La valeur de la capacité minimum mesurable avec l'oscilloscope est de 5 nF

Test de diodes

0 ... 2 V

Test de continuité

< 30 Ω

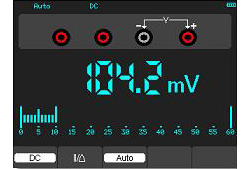
L'oscilloscope PCE-DSO 8060 permet d'utiliser ce dispositif comme multimètre. Cet oscilloscope est capable de mesurer la tension, le courant, la résistance, la capacité et les autres paramètre. La visualisation se produit à travers du grand écran LCD.
En plus de la valeur numérique, l'oscilloscope permet de visualiser un graphique en barres pour l'orientation de la valeur sur la plage de mesure. De même il informe l'usager de la prise à laquelle il doit connecter les câbles d'essai.

Vidéo de l'usage de l'oscilloscope

Caractéristiques techniques du générateur de fonctions de l'oscilloscope PCE-DSO 8060

Plage de fréquence

1 Hz (DC) - 25 MHz

Résolution de fréquence

0,1 %

Temporisateur digital / convertisseur analogique

2 kHz ... 200 MHz

canaux de sortie

un canal

Mémoire

4 KSamples

Résolution verticale

12 bits

Stabilité

< 30 ppm

Amplitude

max. ± 3,5 V

Impédance de sortie

50 Ω

Courant de sortie

50 mA Is= 100 mA

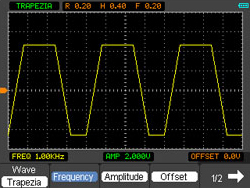
Le générateur de fonctions incorporé dans l'oscilloscope PCE-DSO 8060 permet la sortie par un canal et la simulation de différentes formes d'ondes. L'oscilloscope est capable de simuler les signaux de sortie synodaux, les ondes triangulaires, les ondes carrées, à impulsions ou flancs. L'usager pourra sélectionner librement la fréquence et l'amplitude. En plus d'une simple sortie de signaux, il est possible d'effectuer différentes modulations et modifications de signaux dans l'oscilloscope.

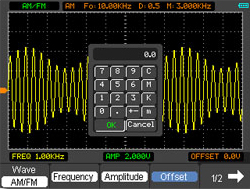
Le vaste menu de l'oscilloscope permet un réglage rapide et simple du générateur de fonctions. Avec un clavier numérique il est possible de régler directement tous les paramètres comme fréquence de sortie et tension de sortie. En utilisant l'oscilloscope comme générateur de fonctions il permet un travail rapide et surtout précis. Sur l'image ci-jointe vous pourrez observer le réglage de la fréquence et l'amplitude d'une forme d'onde de avec modulation FM, effectuée avec le clavier numérique comme décrit ci-dessus.

Spécifications générales de l'oscilloscope PCE-DSO 8060

Ecran

LCD de 5,7" à illumination LED

Résolution de l'écran

240 x 230 pixels

Interfaces

USB (oscilloscope <-> crayon USB)

USB (oscilloscope <-> ordinateur)

Alimentation

Composant de réseau externe:
Entrée: 100 V ... 240 V AC / 50 Hz ... 60 Hz
Sortie: 8,5 V / 1500 mA

Accumulateur ion-lithium intégré:
durée de fonctionnement d'environ 6 h

Dimensions de l'oscilloscope

245 x 163 x 52 mm

Poids

1200 g

L'oscilloscope PCE-DSO 8060 a été conçu pour un usage rapide et simple. Cet oscilloscope a un domaine d'application dans le laboratoire et l'atelier. Grâce à l'intégration de nombreuses fonctions telles que le multimètre, le générateur de fonctions et l'oscilloscope, le PCE-DSO 8060 à un usage très versatile. Son utilisation est très simple et son grand écran permettent une opération de façon rapide, sans que l'usager ait à étudier à fond la notice d'emploi.

En plus de l'oscilloscope même avec fonction de multimètre et générateur de fonctions, les câbles d'essai sont inclus. Avec l'oscilloscope un adaptateur de courant est aussi livré, ainsi qu'une pochette de transport commode et la notice d'emploi détaillée. La pochette de transport protège l'oscilloscope pendant le transport. Grâce aux trois fonctions incorporées dans l'oscilloscope PCE-DSO 8060, les techniciens n'auront pas à porter les trois dispositifs séparément: un oscilloscope, un multimètre et un générateur de fonctions, dans sa boîte à outils. Cela économisera de l'espace et surtout des coûts.

Contenu de la livraison de l'oscilloscope

1 x Oscilloscope PCE-DSO 8060
2 x Sondes pour l'oscilloscope
2 x Câbles de test de laboratoire
1 x Câble de connexion BNC
1 x Composant de réseau électrique
1 x Batterie ion-lithium
1 x Notice d'emploi de l'oscilloscope
1 x Logiciel

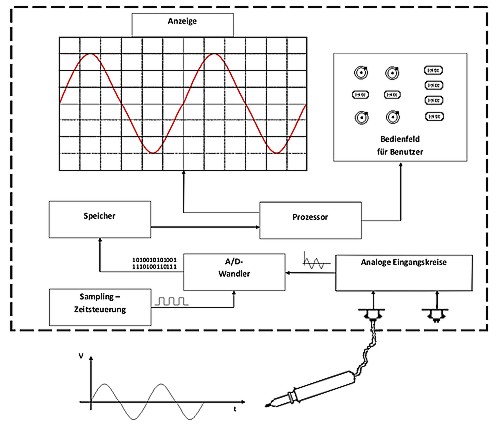
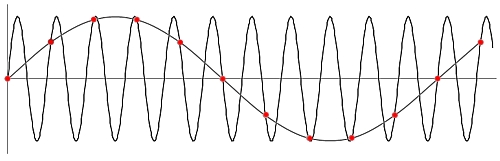
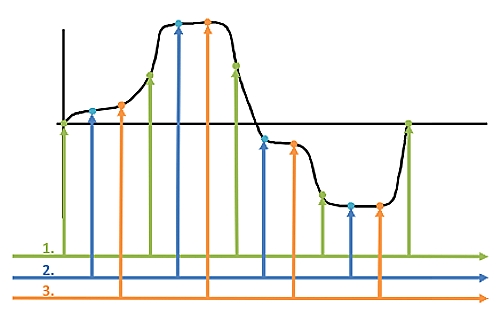
Principe de fonctionnement de l’oscilloscope digital à mémoire
L'oscilloscope s’utilise quand il est nécessaire de représenter les signaux électriques d’une façon visuelle. Le parcours de la tension est représenté à travers le temps dans un système de coordonnées bidimensionnel. Un oscilloscope digital à mémoire est composé de la façon suivante

Le signal recueilli par la pointe de la sonde se règle avec les circuits d’entrée analogique (signal, amplificateur, etc.). Ensuite, il est envoyé à un transducteur A/D. Le transducteur A/D est une pièce qui transforme la tension d’entrée analogique en une valeur numérique digitale. Le signal est vérifié dans un cycle fixe. Les valeurs sont gardées dans une mémoire. Grâce à un processeur, les valeurs se lisent et sont montrées à l’écran.

Certains concepts de l’oscilloscope

Vitesse d’échantillonnage: La vitesse d’échantillonnage vous indique le nombre de fois que le signal analogique est vérifié ou mesuré. Normalement la quantité d’échantillons pris par seconde est indiquée, par exemple 500 MS/s (Megasamples par seconde). De la vitesse d’échantillonnage dépend jusqu’où est montrée une indication correcte de la fréquence du signal d’entrée. Pour obtenir une bonne présentation, la vitesse d’échantillonnage devrait être le décuple de la fréquence d’entrée maximum.
Quand un signal est vérifié avec une faible vitesse d’échantillonnage, l’effet aliasing se produit. Cet effet fait qu’une forme d’onde soit montrée avec le multiple de la période du signal réel. Le croquis suivant l’illustre:

Les points rouges indiquent l’échantillonnage. A partir de celui-ci, un signal acoustique de faible fréquence est reconstruit par erreur. Pour l’éviter, il est possible d’utiliser un filtre à faible passage dans l'oscilloscope qui filtre des fréquences qui sont supérieures à la fréquence d’échantillonnage moyen.

Séquence de mesure (échantillonnage déphasé): Par la séquence de mesure, il est possible de reconstruire correctement des signaux périodiques à une faible vitesse d’échantillonnage. Pour cela chaque période est échantillonnée plusieurs fois. Cependant, les moments de l’échantillonnage se déphasent par rapport au début de la période.

Après la première exécution (en vert) le signal est encore échantillonné plusieurs fois en déphasé (en bleu et orange). Cela permet de reconstruire le signal avec précision bien qu’il y ait une faible vitesse d’échantillonnage. Ce procédé a l’inconvénient que le signal doit être périodique et répétitif. Des évènements uniques et brefs ne peuvent être enregistrés.

Déclenchement (trigger): Si l’oscilloscope indiquerait le signal d’entrée de gauche à droite, il serait impossible de créer une image arrêtée. Etant donné que la fréquence d’image est généralement très élevée et le signal commencerait d’un point quelconque, nous obtiendrions une image intermittente. Pour régler ce problème un trigger est créé. Cela permet d’obtenir une image nette, puisqu’il détecte quand le signal d’entrée dépasse la valeur limite (ce réglage est effectué dans l’oscilloscope). Dès qu’un évènement trigger est créé, le signal d’entrée est montré à l’écran. On obtient ainsi le signal qui sera montré en commençant toujours du même point. De nombreux oscilloscopes vous offrent un déclenchement externe. Cela permet au commencement de l’indication de se régler à travers une entrée externe. L’oscilloscope digital moderne vous offre d’autres possibilités de déclenchement (trigger).

- Certificat de calibrage ISO (calibrage et certificat de laboratoire)
Vous pourrez obtenir un certificat de calibrage ISO de l'oscilloscope. Dans le certificat et le calibrage de laboratoire pour l'oscilloscope, un certificat de révision avec les données de votre entreprise est délivré, pour que vous puissiez par exemple enregistrer les appareils en tant qu'instruments de contrôle ISO, et dans lequel il est certifié que ces appareils peuvent être à nouveau réglés selon les standards nationaux. Vous trouverez à la suite de plus amples informations sur le calibrage:

Calibrage: révision de la précision des magnitudes mesurées de l'oscilloscope sans intervention du système de mesure. Ou bien: détermination de la déviation systématique de l'écran du mesureur par rapport à la valeur réelle de la magnitude mesurée.

Certificat de calibrage: il documente les caractéristiques techniques de mesure de l'oscilloscope ainsi comme le tour de réglage aux standards nationaux.

Intervalle de calibrage: Pour pouvoir effectuer des mesures correctes, l'oscilloscope utilisé devra être révisé ou calibré périodiquement. Cette période de temps correspond à un intervalle de calibrage. Il n'existe pas de norme qui affirme quand il faut recalibrer l'oscilloscope. Il faut prendre en compte au moment de déterminer l'intervalle les points suivants: Magnitude mesurée et bande de tolérance permise

- Utilisation de l'oscilloscope
- Fréquence d'emploi de l'oscilloscope
- Conditions environnementales de l'oscilloscope
- Stabilité du calibrage antérieur de l'oscilloscope
- Précision de mesure exigée de l'oscilloscope
- Dispositions relatives au système de contrôle de qualité en entreprises de l'oscilloscope

Cela signifie que la période entre deux calibrages doit être fixée et contrôlée par le propre usager. Nous conseillons pour l'oscilloscope un intervalle de calibrage d'entre 1 et 3 ans. Pour toute assistance aux clients désirant augmenter la fixation de l'intervalle, nos employés vous conseilleront avec plaisir.

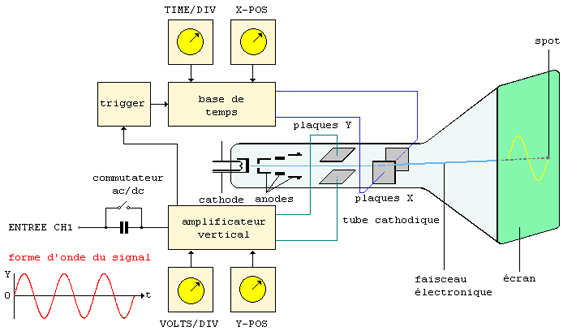
Principe de fonctionnement de l'oscilloscope digital
Quand nous avons un circuit et nous désirons observer la réponse du signal qui en résulte, il faudra connecter une sonde à l'élément que nous voulons vérifier pour voir le résultat de ce circuit ou son composant. Le signal ira de la sonde à la section verticale, que nous pourrons amplifier ou atténuer grâce aux commandes digitales dont dispose l'oscilloscope. Une fois le signal amplifié, grâce au module antérieur, il s'enverra à la section horizontale pour que, grâce à ce pas et au pas précédent et grâce aussi aux différents procédés tels que les convertisseurs A/D, l'écran montre le signal recherché. Si la tension de ce signal est positive en référence avec le point de référence ou GND, il sera indiqué dans la partie supérieure de l'écran et par contre si elle est négative, il sera indiqué dans la partie inférieure.
Comme indiqué ci-dessus, le signal passe de la sonde jusqu'à la section verticale, et de celle-ci il passe à la section horizontale, non sans passer avant par la section de déclenchement qui est chargée de bouger le signal de la partie gauche à la partie droite d'un temps déterminé (grâce à cela il est aussi possible d'obtenir une stabilisation du signal). Ce parcours est obtenu grâce à la base du temps (TIME-BASE).
Les réglages de base devant s'effectuer pour une utilisation correcte de l'oscilloscope sont:

- Commande Ampli. (atténuation ou amplification) - Cette commande règle l'amplitude du signal
  ou des signaux dépendants de l'oscilloscope dont on dispose. Il faut que le signal occupe
  tout l'écran sans dépasser les limites de celle-ci.

- Commande Timebase (échelle de temps) - Cette commande règle le temps par quadrillage
  représentée par une division de l'écran.

- Commande Trigger Level et Trigger Selector (niveau de déclenchement / type de déclenchement) -  Avec ces commandes il est possible d'obtenir la meilleure stabilisation possible des signaux qui
  se répètent plusieurs fois.

- De plus il est aussi très important de régler les paramètres de mise au point, d'intensité et
  de positionnement des signaux dans les axes X et Y.

L'oscilloscope digital en plus de ces réglages possède une mémoire pour effectuer des mesures prolongées et pouvoir transférer ces données à un PC.

Principe de fonctionnement d'un oscilloscope

Loi d'Ohm
George Simon Ohm fut un physicien allemand célèbre pour ses recherches sur les courants électriques. Sa formulation de la relation entre l'intensité du courant, la différence de potentiel et la résistance contribue à la loi d'Ohm, avec laquelle il établit dans sa loi que la quantité de courant qui circule par un circuit formé par des résistances pures est directement proportionnel à la force électromotrice appliquée à un circuit, et inversement proportionnel à la résistance totale du circuit. Cette loi est normalement exprimée avec la formule I= V/R, où I représente l'intensité du courant mesuré en ampères, V la force électromotrice en volts et R la résistance en ohms.
L'unité de résistance électrique a été appelé ohm en son honneur et fut définie en 1893.
La loi d'Ohm n'est pas une loi naturelle fondamentale mais une relation empirique valable uniquement pour certains matériaux. Les matériaux qui ont une constante de résistance sur une vaste plage de voltages et les matériaux qui ne suivent pas cette loi sont appelés non linéaires et ont une relation de courant-voltage non linéaire. Les matériaux qui suivent cette loi s'appellent conducteurs ohmiques ou conducteurs linéaires et ont une relation de courant-voltage sur une vaste plage de voltages appliqués.
La loi d'Ohm est la loi de base pour le flux du courant. Le courant flue par un circuit électrique en suivant plusieurs lois.
Qu'est-ce qu'un un circuit série?
Un circuit signifie que les dispositifs ou les éléments du circuit sont disposés de façon à ce que la totalité du courant passe à travers de chaque élément sans division ni dérivation dans des circuits parallèles.
Cette loi s'applique à tous les circuits électriques de courant continu et de courant alternatif, bien que pour analyser des circuits plus complexes il faut utiliser d'autres principes supplémentaires à cette loi.
Actuellement pour résoudre théoriquement les circuits électroniques on prend comme référence que le courant doit toujours circuler du sens positif au négatif. Récemment il a été démontré que le sens réel que ces électrons suivent est tout à fait le contraire: du négatif au positif mais pour la résolution théorique de ces circuits ce qui est toujours pris en compte est du sens positif au sens négatif, c'est-à-dire suivant la loi d'Ohm.

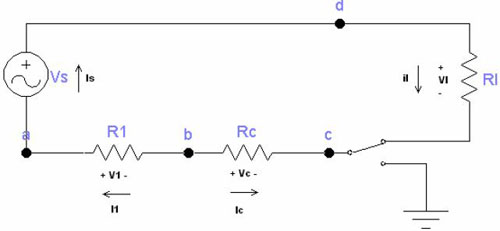
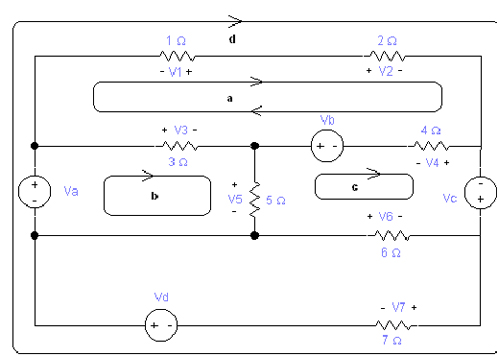
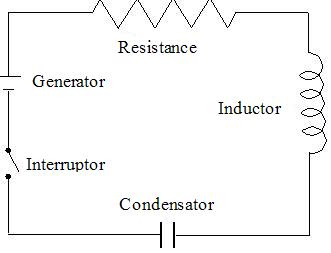
Circuit électrique
Avec un oscilloscope il est possible de vérifier un circuit électrique. Un circuit électrique est une série d'éléments électriques ou électroniques, comme par exemple des résistances, des inductances, des condensateurs, des dispositifs électroniques semi conducteurs,... connectés électriquement entre eux afin de générer, transporter ou modifier des signaux électroniques ou électriques. On dit donc qu'un circuit est résolu quand le voltage et le courant sont déterminés à travers de chaque élément. La loi d'Ohm (comme indiqué précédemment) est une équation importante pour déterminer la solution. Cependant, cette loi peut ne pas être suffisante pour proportionner une solution complète. Comme vous pouvez le voir sur la photo ci-dessous, pour essayer de résoudre le circuit il est nécessaire d'utiliser les lois de Kirchhoff, comme pour la plupart des circuits.

Comme vous pouvez le voir, les variables des courants et des voltages associés à chaque résistance et le courant associé à la source de voltage on été marqués (le marquage comprend les polarités de référence). Les points indicateurs des pôles sont les points du début et de la fin d’un élément de circuit individuel. Un nœud est un point où se trouvent deux éléments ou plus de circuit. Comme indiqué ci-dessous, il est nécessaire d’identifier les nœuds pour utiliser la loi du courant de Kirchhoff. Sur la figure 1.1 les nœuds sont a, b, c et d. Le nœud d connecte la batterie au foyer et par essence il s’étend sur toute la partie supérieure du diagramme, bien que l’on utilise qu’un seul point par commodité. Les points de chaque côté de l’interrupteur indiquent ses pôles, mais seul un est nécessaire pour représenter un nœud, alors on en indique qu’un comme étant le nœud c.

Pour le circuit représenté sur la figure 1.1 nous pouvons identifier sept inconnues: Is, I1, Ic, il, V1, Vc et Vl. On rappelle que Vs est un voltage connu car il représente la somme des voltages entre les pôles des deux cellules sèches, un voltage constant de 3V. Le problème est qu’il faut trouver les sept variables inconnues. De par l’algèbre nous savons que pour trouver n quantités inconnues, il faut résoudre n équations simultanées indépendantes. La loi d’Ohm nous indique que trois des équations nécessaires sont: V1 = I1 x R1 / Vc = Ic x Rc / Vl = il x Rl

L’interconnexion d’éléments du circuit impose certaines restrictions en relation entre les voltages et les courants. Ces restrictions sont connues comme les lois de Kirchhoff, en l’honneur de Gustav Kirchhoff qui fut le premier à les établir dans un article publié en 1948. Les 2 lois qui établissent les restrictions mathématiquement sont connues sous le nom de loi de Kirchhoff des nœuds et loi de Kirchhoff des mailles.

Nous pouvons maintenant énoncer la Loi de Kirchhoff des nœuds:

La somme algébrique de tous les courants dans
n’importe quel nœud d’un circuit est égale à 0

Pour utiliser la loi de Kirchhoff des nœuds, il faut attribuer à chaque courant du nœud un signe algébrique selon un sens de référence. Si l’on attribue un signe positif à un courant qui sort du nœud, il faudra attribuer un signe négatif à un courant qui entre dans le nœud. Au contraire, si l’on détermine un signe négatif à un courant qui sort du nœud, il faudra attribuer un signe positif à un courant qui entre dans le nœud.

En appliquant la loi de Kirchhoff des nœuds pour les quatre nœuds du circuit de la figure 1.1,et en utilisant la conversion qui établit que les courants qui sortent du nœud sont considérés positifs, on obtient quatre équations:

- Nœud A –-> Is – I1 = 0       (Equation 1.5)
- Nœud B –-> I1 + Ic = 0      (Equation 1.6)
- Nœud C –-> - Ic – il = 0     (Equation 1.7)
- Nœud D –-> il – Is = 0       (Equation 1.8)

Observez que les équations 1.5 – 1.6 – 1.7 – 1.8 ne forment pas un système indépendant parce qu’elles peuvent toutes les quatre s’obtenir des trois autres. Dans n’importe quel circuit ayant n nœuds, on peut dériver n – 1 équations de courant indépendantes de la loi des nœuds de Kirchhoff. Si nous ne prenons pas en compte l’équation 1.8 nous avons 6 équations indépendantes, c’est-à-dire, les équations de 1.2 à 1.7. Mais nous en avons besoin d’une autre que nous pouvons obtenir de la loi des mailles de Kirchhoff.

Avant d’énoncer la loi de Kirchhoff des mailles, nous devons définir ce qu’est une trajectoire fermée. En commençant par un nœud choisi arbitrairement, nous traçons une trajectoire fermée dans un circuit à travers d’éléments de base sélectionnés du circuit et nous retournons au nœud d’origine sans passer par aucun autre nœud intermédiaire plus d’une fois. Le circuit de la figure 1.1 a une trajectoire fermée. Par exemple, si on prend le nœud a comme point de départ, et l’on parcourt le circuit dans le sens des aiguilles d’une montre, nous formons une trajectoire fermée en passant par les nœuds d, c, b, et en retournant au nœud a.

Maintenant nous pouvons énoncer la Loi des Mailles de Kirchhoff:

La somme algébrique de tous les voltages autour
de toute trajectoire fermée d’un circuit est égale à 0

Pour utiliser la loi des mailles de Kirchhoff, nous devons attribuer un signe algébrique (un sens de référence) à chaque voltage de la maille. Pendant que nous parcourrons la trajectoire fermée, un voltage apparaitra soit comme élévation ou comme une chute dans le sens du parcours. Si l’on attribue des valeurs positives à des élévations de voltage, il faudra attribuer des valeurs négatives aux chutes de voltages. Au contraire, si des valeurs négatives sont déterminées pour les élévations de voltage, il faudra attribuer des valeurs positives aux chutes de voltage.

Nous appliquons la loi des mailles de Kirchhoff au circuit indiqué sur la figure 1.1. Nous choisissons de tracer la trajectoire fermée dans le sens des aiguilles d’une montre, en attribuant un signe algébrique positif aux chutes de voltage. Si l’on commence dans le nœud d, on obtient l’expression suivante:

Vl – Vc + V1 – Vs = 0

Qui représente la septième équation indépendante nécessaire pour déterminer les sept variables inconnues du circuit mentionné ci-dessus.
Avec ces sept équations nous avons donc la formulation nécessaire pour résoudre les doutes sur les différentes variables. Ce résumé sert à énoncer les lois de Kirchhoff avec lesquelles nous pourrons plus bas et grâce aux techniques analytiques, résoudre les circuits d’une façon plus rapide et simple.

Pour finir, nous verrons un petit résumé des pas à suivre pour obtenir une analyse d’un circuit.

Tout d’abord, observez que si vous connaissez le courant d’une résistance, vous connaissez le voltage à travers elle, étant donné que le courant et le voltage sont directement liés par la loi d’Ohm. Ainsi, vous pourrez associer une seule variable inconnue à chaque résistor, soit du voltage ou du courant. Sélectionnons le courant comme variable inconnue. Alors, une fois résolu le courant inconnu du résistor, vous pourrez trouver le voltage à travers du résistor. En général si l’on connait le courant dans un élément passif, vous pouvez trouver le voltage à travers lui, en réduisant d’une façon importante le nombre d’équations simultanées à résoudre. Par exemple, dans le circuit de la figure 1.1, nous éliminons les voltages Vc, Vl et V1 comme inconnues. Ainsi, à la fin la tâche analytique se réduit à résoudre quatre équations simultanées au lieu de sept.

La seconde observation générale est en relation avec les conséquences de connecter uniquement deux éléments pour former un nœud. Selon la loi de Kirchhoff des nœuds, quand seuls deux éléments sont connectés à un nœud, si l’on connait le courant de l’un des éléments, on connait aussi le courant du second élément. C’est-à-dire, il faut définir uniquement un courant inconnu pour les deux éléments. Quand uniquement les deux éléments se connectent à un seul nœud, on dit que les éléments sont en série. L’importance de cette seconde observation est évidente quand vous voyez que chaque nœud du circuit indiqué sur la figure 1.1 implique uniquement deux éléments. Il ne faut donc définir que le courant inconnu. La raison est que les équations 1.5 – 1.6 et 1.7 conduisent directement à

Is = I1 = - Ic = il

Ce qui établit que si l’on connait le courant de certains éléments, on connait celui de tous. Par exemple, si nous décidons utiliser Is come inconnue, on élimine I1, Ic et il. Le problème se réduit à déterminer une inconnue, c’est-à-dire Is.

L’exemple ci-dessous illustre comment écrire les équations des circuits en se basant sur les lois de Kirchhoff.

Exemple

Additionnez les voltages autour de chaque trajectoire désignée dans le circuit indiqué sur la figure 1.2.

Figure 1.2 (Le nœud d va dans tout le circuit)

Solution:

En écrivant les équations, nous utilisons un signe positif pour les chutes de voltage.
Les quatre équations sont:

- Trajectoire a → V1 + V2 + V4 – Vb – V3 = 0
- Trajectoire b → Va + V3 + V5 = 0
- Trajectoire c → Vb – V4 – Vc – V6 – V5 = 0
- Trajectoire d → Va – V1 + V2 – Vc + V7 – Vd = 0

Sur la photo ci-dessus nous pouvons voir un circuit électrique simple mais complet, en ayant les trois parties fondamentales: un interrupteur qui allume et éteint le circuit, une source d'énergie électrique, dans ce cas la pile ou la batterie et enfin une application, dans ce cas une résistance ou un inducteur et un condensateur.

Si vous désirez voir ou imprimer la section de notre catalogue correspondant à l'oscilloscope,
veuillez cliquer sur le symbole PDF.

Vous aurez ici une vision générale de tous les mesureurs proposés par PCE France

Contact:
PCE Instruments France EURL
23, rue de Strasbourg
67250 SOULTZ-SOUS-FORETS
France
tél. +33 (0) 972 3537 17
fax +33 (0) 972 3537 18

A continuation vous pourrez trouver une vision générale des groupes de produits des Mesureurs: